{TITRE}
Fiche explicative à télécharger gratuitement sur le chapitre de maths du tronc commun des Bacs Pro : La Trigonométrie.
consulter ce formulaire de trigonométrie

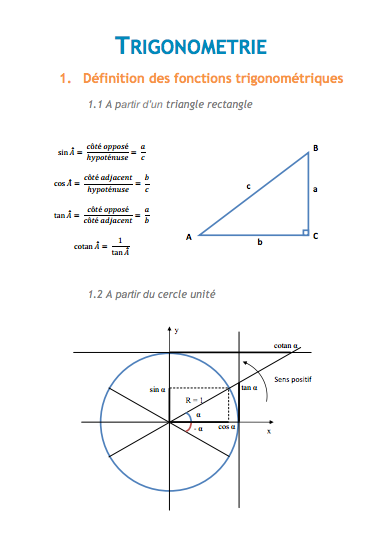
- Sin(α) est égal à la projection orthogonale du rayon sur l'axe y.
- Cos(α) est égal à la projection orthogonale du rayon sur l'axe x.
- Tan(α) est déterminé par l'intersection entre le prolongement du rayon et la droite parallèle à l'axe y et coupe l'axe x au point (1,0).
- Cotan(α) est déterminé par l'intersection entre le prolongement du rayon et la droite parallèle à l'axe x et coupe l'axe y au point (0,1).
En regardant le dessin au dessus, on peut en déduire les relations entre les angles :
 sin(-α) = -sin(α) cos(-α) = cos(α) tan(-α) = -tan(α)
 sin(π + α) = -sin(α) cos(π + α) = -cos(α) tan(π + α) = tan(α)
 sin(π - α) = sin(α) cos(π - α) = -cos(α) tan(π - α) = -tan(α)
 sin(π/2 - α) = cos(α) cos(π/2 - α) = sin(α)
 etc...
- Quand l'angle α tend vers 0, tan(α) tend vers sin(α) et les deux tendent vers α.
- Quand l'angle α tend vers 90°, tan(α) tend vers l'infini.
Relation entre les carrés :
(Pour voir les formules et figures correctement, télécharger la fiche complète gratuitement en cliquant sur le bouton "Voir ce document")
Formules d'addition :
(Pour voir les formules et figures correctement, télécharger la fiche complète gratuitement en cliquant sur le bouton "Voir ce document")
Formules de duplication :
(Pour voir les formules et figures correctement, télécharger la fiche complète gratuitement en cliquant sur le bouton "Voir ce document")
Les expressions de cosinus, sinus et tangent en fonction de la tangente de l'angle moitié :
Formules de linéarisation :
(Pour voir les formules et figures correctement, télécharger la fiche complète gratuitement en cliquant sur le bouton "Voir ce document")
Remarque :
Il faut simplement mémoriser les trois premières formules pour en déduire toutes les autres.
Exemples
1/ cos(2α) = cos(α + α) = cos(α).cos(α) - sin(α).sin(α) = cos2(α) - sin2(α)
= cos2(α) - (1-cos2(α)) = 2cos2(α) - 1
On en déduit cos2(α) = 1/2 (cos(2α) + 1)
2/ cos(a - b) = cos(a+(-b)) = cos(a)cos(-b) - sin(a)sin(-b) = cos(a).cos(b) + sin(a).sin(b)
3/ On a :
cos(a+b) = cos(a).cos(b) - sin(a).sin(b)
cos(a - b) = cos(a).cos(b) + sin(a).sin(b)
En sommant les deux équations, on obtient donc cos(a).cos(b) = 1/2 [cos(a+b) + cos(a - b)]
On pose x = a + b, y = a - b. Donc a = (x+y)/2 et b = (x-y)/2
On en déduit la relation : cos(x) + cos(y) = 2. cos(( x+y)/2).cos((x-y)/2)
c^2= a^2+b^2-2ab.cosâ¡C Ì‚
(Pour voir les formules et figures correctement, télécharger la fiche complète gratuitement en cliquant sur le bouton "Voir ce document")
a/sinâ¡A Ì‚ = b/sinâ¡B Ì‚ = c/sinâ¡C Ì‚
(Pour voir les formules et figures correctement, télécharger la fiche complète gratuitement en cliquant sur le bouton "Voir ce document")
Vous devez être connecté pour pouvoir lire la suite
 Seconde professionnelle : programme de mathémat...
Seconde professionnelle : programme de mathémat...
En Seconde professionnelle, l'enseignement des mathématiques permet aux élèves d...
23/04/2019 10h51 Seconde pro : le programme de Français
Seconde pro : le programme de Français
L'enseignement du Français fait partie des matières générales inclues au program...
23/04/2019 10h43 Seconde professionnelle : le programme de Physi...
Seconde professionnelle : le programme de Physi...
En seconde professionnelle, l'enseignement de la Physique-chimie est inclus au p...
18/04/2019 10h47 Seconde pro : programme de prévention santé env...
Seconde pro : programme de prévention santé env...
Le programme de seconde professionnelle intègre la matière prévention santé envi...
15/04/2019 15h20Vous devez être membre de digiSchool bac Pro
Pas encore inscrit ?
Ou identifiez-vous :