Fiche de révision sur la fonction dérivée : chapitre du programme du tronc commun de maths de Bac Pro.

Ce cours de maths est à télécharger gratuitement et à conserver pour vos révisions du Bac Pro en maths !

Fonction dérivée

1. Définitions

1.1 Fonction dérivée

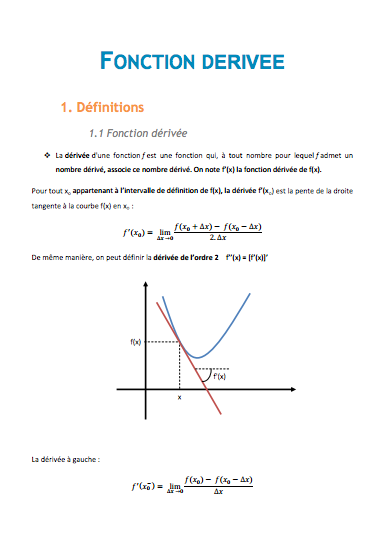
La dérivée d'une fonction f est une fonction qui, à tout nombre pour lequel f admet un nombre dérivé, associe ce nombre dérivé. On note f’(x) la fonction dérivée de f(x).

Pour tout x_o appartenant à l’intervalle de définition de f(x), la dérivée f’(x_o) est la pente de la droite tangente à la courbe f(x) en x_o :

(Pour voir les formules et figures correctement, télécharger la fiche complète gratuitement en cliquant sur le bouton "Voir ce document")

De même manière, on peut définir la dérivée de l’ordre 2              f’’(x) = [f’(x)]’

La dérivée à gauche :

(Pour voir les formules et figures correctement, télécharger la fiche complète gratuitement en cliquant sur le bouton "Voir ce document")

La dérivée à droite :

(Pour voir les formules et figures correctement, télécharger la fiche complète gratuitement en cliquant sur le bouton "Voir ce document")

1.2 Dérivabilité

Une fonction est dérivable en un point x si et seulement si ses dérivées de gauche et de droite existent et elles sont égales.

1.3 L’intervalle de dérivabilité

L’intervalle de dérivabilité d’une fonction est l’intervalle ou la fonction admet une dérivée.

2. Propriétés

2.1 Continuité et dérivabilité

Si une fonction est dérivable en un point x, alors elle est continue en x.

Par contre, si une fonction est continue en x, on ne peut pas conclure sur sa dérivabilité.

Remarque : A priori, les fonctions usuelles sont dérivables sur l’intervalle de continuité.

2.2 Comportement d’une fonction

Soit f une fonction continue et dérivable sur D. 

-          Si la dérivée f’ est positive, alors la fonction f est croissante

-          Si la dérivée f’ est négative, alors la fonction f est décroissante.

-          Si la dérivée f’ est nulle :

o   la fonction admet un maximum local en  si f’’() < 0

o   la fonction admet un minimum local en  si f’’() > 0

o   la fonction admet un point de flexion en  si f’’() = 0

(Pour voir les formules et figures correctement, télécharger la fiche complète gratuitement en cliquant sur le bouton "Voir ce document")

Exemple : Etudier le comportement de la fonction f(x) = x² + 3. On a :

f'(x) = 2x et f’(x) = 0 ó x = 0.

La fonction admet un minimum en 0 et f(0) = 3.

3. Dérivées des fonctions usuelles :

(Pour voir les formules et figures correctement, télécharger la fiche complète gratuitement en cliquant sur le bouton "Voir ce document")

4. Opérations et dérivées

u et v sont deux fonctions dérivables sur un intervalle I :

Tous nos cours maths Bac Pro sont disponibles sur le site entièrement gratuitement !